Risk Reversals - Global Financial Markets Institute

Risk reversal is a commonly used term in the FX markets. Specifically, a risk reversal is:

An option strategy combining the simultaneous purchase of out-of-the-money calls (puts) with the sale of out-of-the money puts (calls). The options will have the same expiration date and similar deltas.
A market view on both the underlying currency and implied volatility.

This article:

Describes the origins of the risk reversal
Defines the volatility smile and skew
Examines specific example of quotes
Investigates a hedging example

Origins of the Risk Reversal

The risk reversal has it underpinnings from the limitations of the Black Scholes Merton (BSM) option pricing model. One of the limitations is that the BSM assumes a normal distribution. Anyone involved in the spot FX markets will tell you that price ranges are anything but normal! In practice, the currency markets follow what is known statistically as leptokurtosis. In laymen’s terms, this means that the underlying will trade at extreme prices from the current spot market more frequently than a normal distribution would suggest. The price action at these extreme levels is referred to as “fat tails”.

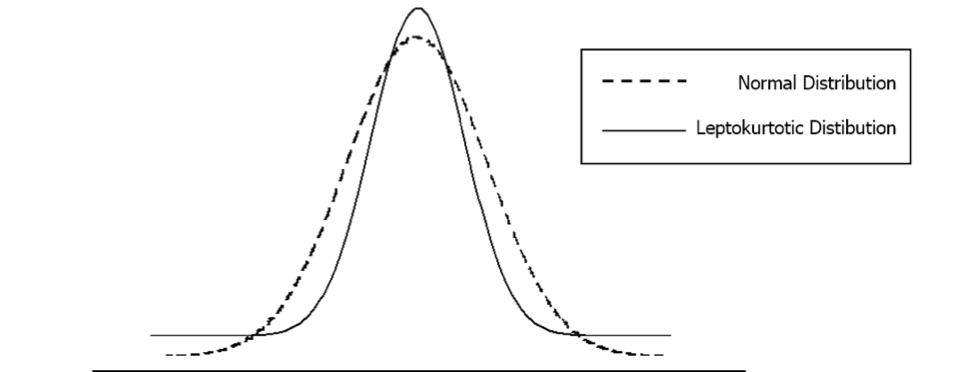
Riskreversal

Figure 1: Normal Distribution vs. Leptokurtotic Distribution

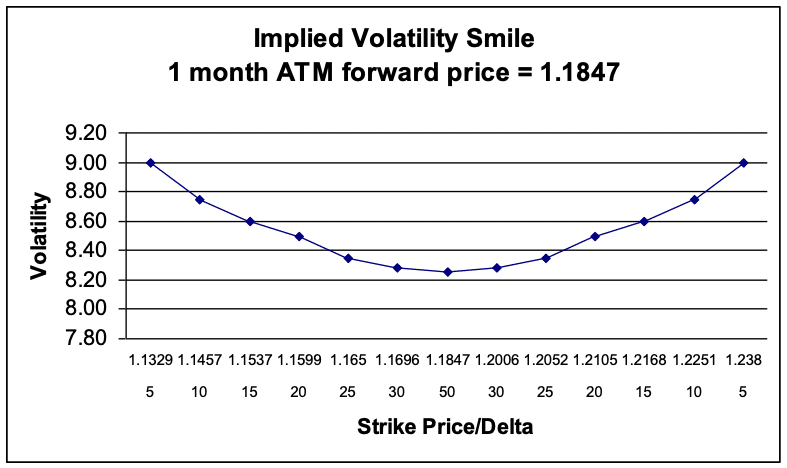
Volatility Smile

If more price action occurs at these extreme levels than suggested by the model, the option trader will mark volatility higher to account for the increased probability of the underlying trading in the “fat tails”. The end result is that implied volatility will be higher for out-of-money (OTM) and in-the-money (ITM) options then at-the-money (ATM) options. If there is no bias in market expectations of the underlying price, then the picture of volatility is symmetrical around the at-the-money volatility. This is commonly referred to as the “volatility smile”. Notice in Figure 2 how the volatilities are symmetrical around the ATM forward.

Figure 2: Theoretical Volatility Smile – USD/CAD

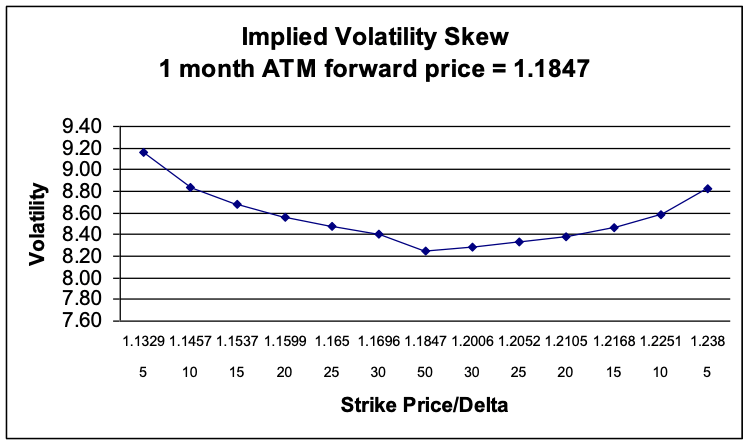
Volatility Skew

In practice there are supply and demand considerations along with market expectations built into option prices. This pushes up the volatility for ITM (OTM) calls (puts) relative to those of the puts (calls). This is referred to as the “skew”. The risk reversal expresses the difference in volatility. In theory, if a currency is expected to appreciate, calls would be favored over puts and the purchaser of the call would pay a higher volatility relative to puts.

Figure 3: Volatility Skew – USD / CAD Source: Superderivatives

Looking at Figure 3, notice how the volatilities are higher as the CAD is appreciating. The interpretation is that the market expects the CAD to appreciate and/or implied volatility to move higher.

Example

The market has established a 25 (0.25) delta benchmark for risk reversal quotes. For example, assume the market expects the CAD to appreciate against the USD. A trader quotes a 1-month 25 delta USD/CAD risk reversal of .15 -.28% where CAD calls are favored over CAD puts. Based on this information, the trader would be willing to do each of the following, assuming volatility is 8.50%:

Buy the 25 delta USD put/CAD call at 8.65% and sell the USD call/CAD put at 8.50%. The trader pays away the .15%

Sell the 25 delta USD put/ CAD call at 8.78% and buy the USD call/CAD put at 8.50%. The trader earns the .28 spread

In essence, the dealer is willing to buy the USD put/CAD call at 8.65% and sell the USD put/CAD call at 8.78%. The dealer is giving a “choice” quote to either sell the USD Call/CAD put or buy the USD call/CAD put at 8.50%.

Hedging Example

Assume a U.S. company is importing goods from Germany and is invoiced in euros. The invoice is EUR 1,000,000 and is due in three months. The company is concerned that the USD will depreciate. Assume current market prices are as follows:

Spot	1.2073
Forward	1.2146
EUR Call 25 Delta Strike/Vols	1.2519 / 9.15%
Premium	USD 800

EUR Put Strike/Vols	1.1779 / 8.95%
Premium	USD 800

To hedge the position, the company buys a EUR call/USD put at 25 delta and sells a corresponding EUR put/USD call.

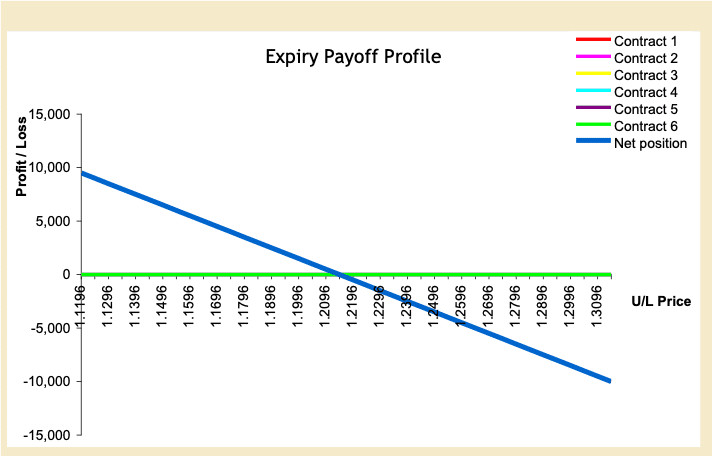
Figure 4 shows the company’s exposure in three months. Assume the current 3-month forward price is 1.2146 and the company could lock in the forward exchange rate at this price. Hence, this will be their benchmark to compare the hedge using the risk reversal.

Figure 4: Net Exposure of U.S. Company

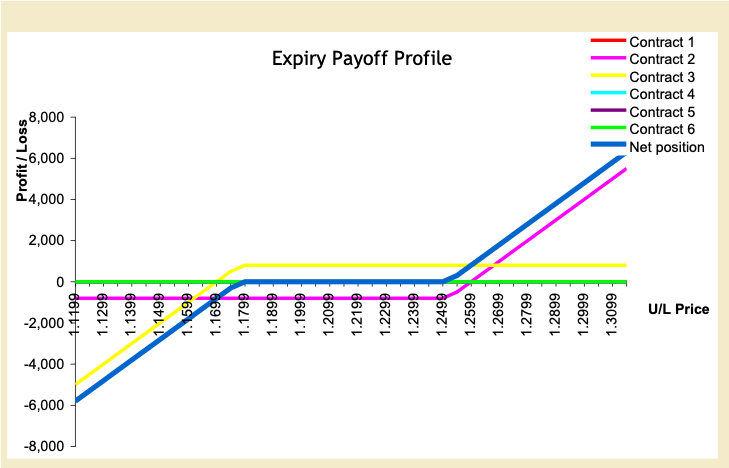
Figure 5 shows the risk reversal. Contract 2 is the EUR call / USD put. Contract 3 is the EUR put /USD call. The blue line is the net position of the two contracts

Figure 5: Risk Reversal

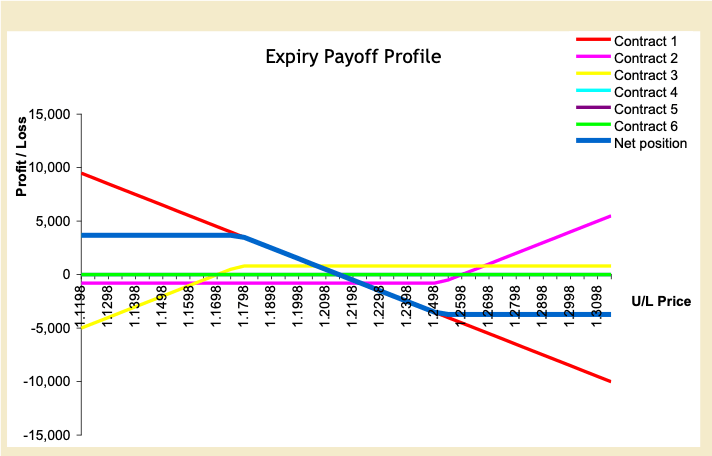
Figure 6 combines the two positions resulting in what is commonly referred to as a collared position. Contract 1 is the company’s original exposure to the euro. Contract 2 is the EUR call / USD put. Contract 3 is the EUR put / USD call. The blue line is the net position of the three contracts (exposures).

Figure 6: Combined Exposure of U.S. Company with Risk Reversal

It is interesting to note that the company is more concerned with the efficacy of the hedge. The trader, on the other hand, will be more interested in the detailed aspects of the risk reversal including the impact it will have on the option books’ risk measurements, i.e. the Greeks.

Summary

This article:

Described the origins of the risk reversal
Defined the volatility smile and skew
Examined specific example of quotes
Investigated a hedging example

Any questions or comments can be addressed to the author at [email protected]

Acknowledgments

I want to thank:

Superderivatives for supplying the data.
Chisholm Roth for using Magellan spreadsheets illustrating the option payoff profiles

About the author

Ken Kapner, CEO and President, started Global Financial Markets Institute, Inc. (GFMI) a NASBA certified financial learning and consulting boutique, in 1998.

Download article